Results
In this study, the density state (i.e., sample labeled as “):dense”, “1:medium”, or “2:loose”) will be used as the name of categories for classification predictions and void ratio were predicted using the previously designed CNN model as regression predictions. All 1224 2D Contact Direction Histogram images were utilized as input data, and the datasets were divided into training and testing sets, with an 80-20 split. Additionally, 20% of the training data was allocated for validation. Loss was calculated using the mean squared error loss function (MSE). The loss graph for void ratio and density state, depicted in Figure 1 and Figure 2, illustrates its decreasing trend as the CNN model learns. Figure 3 presents a comparison between density predictions and actual density labels, while Figure 4 showcases the model predictions for void ratio (regression output).
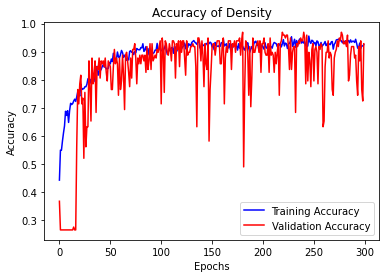
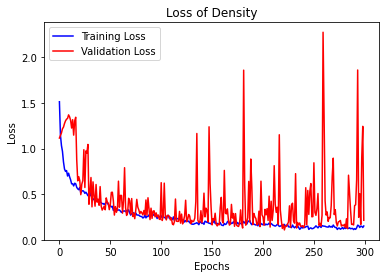
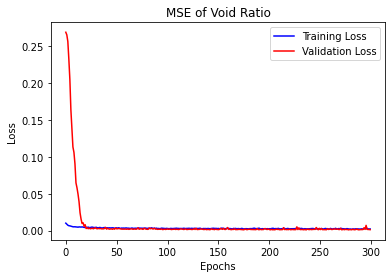
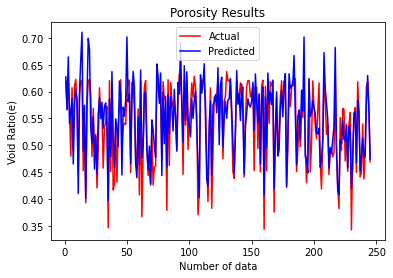
Figure 5 shows the confusion matrix results for the density classification problem.
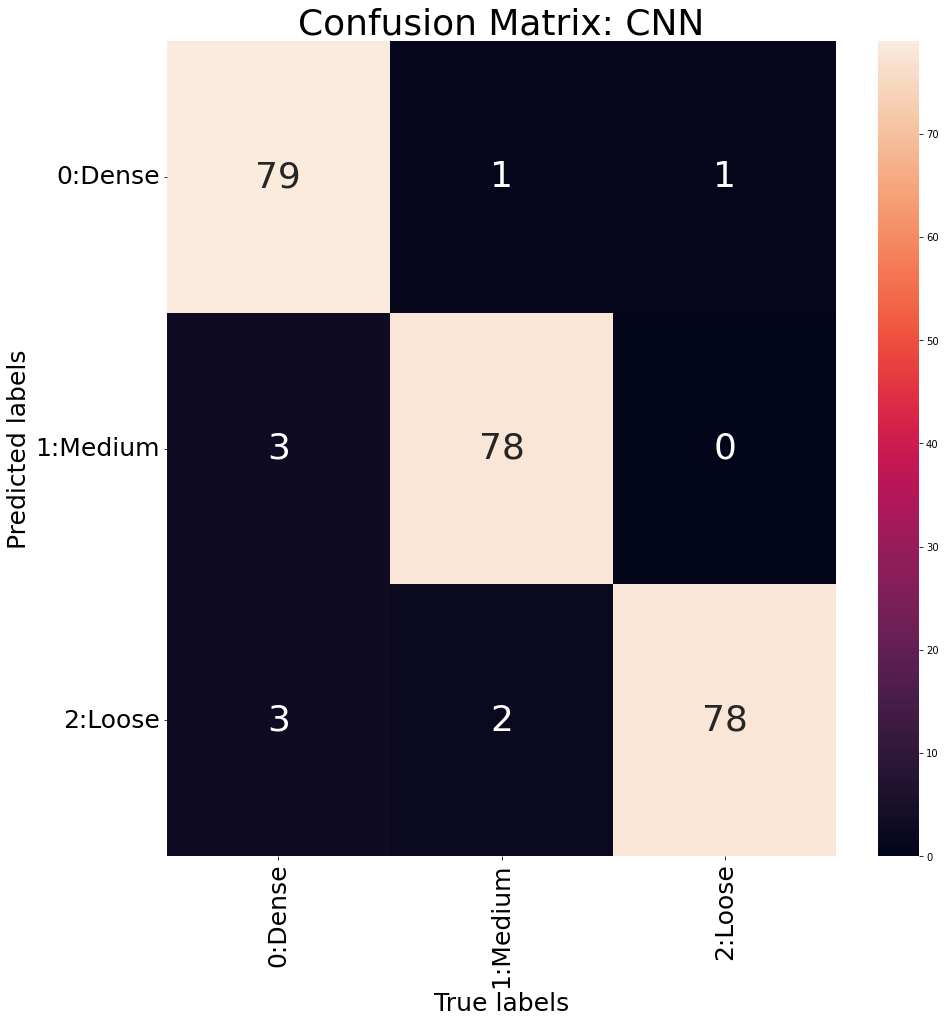
Figure 6 is the representative model prediction results for classification problems and regression problems.
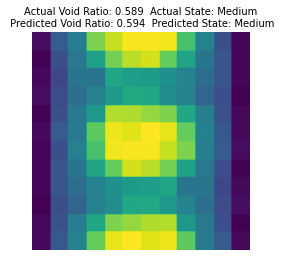
Based on the plots, the main results are as follows:
1) The void ratio test data and predicted data are plotted as ascending sorting. The minimum error percentage between actual void ratio data and predicted void ratio data is `0.0178%` and the maximum error percentage is `23.126%`. The average porosity errorpercentage is `5.69%`.
2) The accuracy of density classification problem is `95.9%` , and MSE of viod ratio regression problem is `0.0015` .
3) The deep learning method based on CNN and its extension has been proven to effectively capture the correlation between fabric direction images and induce the density state and void ratio of granular materials.
4) Deep learning methods can be applied to classification and regression prediction in granular material fabric dataset.
It’s great to find that the designed CNN model is performing well on the prediction tasks for the 2D Contact Direction Distribution Histogram images. The fact that the model can successfully extract features even from images with subtle differences underscores the effectiveness of the CNN structure in capturing intricate details.
The unexpected success, especially given the relatively small size of the input dataset, has sparked my curiosity about utilizing neural networks for studying high-dimensional microscopic information in granular materials. The promising results from this experiment indeed indicate the feasibility of leveraging neural networks for such endeavors.
However, the observation about the fluctuating validation accuracy, particularly in dealing with the density classification problem, raises a valid concern. Fluctuations in validation accuracy are not uncommon, especially in scenarios with small-scale datasets, and they can be attributed to noise in the data. The validation accuracy calculation being based on mini-batches of the validation set might introduce more variability.
To address this issue, we might consider employing techniques such as data augmentation, regularization, or even exploring more advanced architectures to enhance the model’s generalization capabilities. Additionally, increasing the size of the dataset, as mentioned earlier, could potentially help mitigate noise-related fluctuations and contribute to a more stable model performance.