Conclusions
The deep learning model in this study uses convolutional neural networks (CNN) and related task-based structures (CNN-GRU) to perform density classification and void ratio regression prediction on 2D Direction Distribution Histogram images. Like other neural network learning, the model calculation result and loss of each epoch are monitored, the difference between the actual value and the predicted value is calculated, and then the updated value of model parameters is determined through back propagation with the help of differential equations. As the model goes through more iterations, the loss gradually decreases and converges, indicating that the neural network is learning how to better capture the expected data relationships.
Due to the exploratory limitations of this study, no definitive conclusions can be drawn regarding the establishment of a one-to-one physical correlation between porosity and fabrics. To enhance the reliability of findings, it is recommended to incorporate larger datasets and include a variety of experiments, such as simple shear, triaxial, drained, undrained, monotonic, and various looping tests. This approach aims to validate the predictive capabilities of the CNN/CNN-GRU model trained on fabric image data.
The small-scale dataset utilized in this study may not be well-suited for conventional data augmentation methods. Unlike other image training datasets, 2D Fabric Direction Distribution images lack particularly distinct features. Therefore, the advantage of the CNN model to layer different image contours/features through kernel extraction feature maps was significantly limited in this experiment.
Traditional data augmentation for small-scale image datasets typically involves techniques such as stretching, flipping, local shearing, and color changes to generate additional images and expand the dataset. In fact, for the small-scale cat and dog image classification problem dataset, generating upside-down images might not be suitable, as cats or dogs are not typically inverted in real life.
Considering the dataset of this study, 2D Fabric Direction Distribution images lack clearly differentiated classification features. Therefore, it becomes crucial to assess whether traditional data enhancement methods maintain interpretability and physical meaning. For instance, does a flipped image still correspond to the void ratio of the original image? Addressing such questions is imperative for ensuring the applicability of neural networks to fabric image data.
We discovered an fluctuation issue during prediction, which indicated that while the model performed well on the data, it did suffer some noisey indormation with propagation. To address this challenge in future work, we plan to explore alternative approaches to mitigate high variance and low bias problems. This may involve implementing custom regularization techniques, integrating batch normalization, and exploring other strategies.
It is important to emphasize that our input dataset is relatively smaller than typical datasets. In future efforts, we aim to collate a broader dataset containing more fabric orientation information. Using a larger dataset as input is expected to significantly improve the performance of the model. Furthermore, we can leverage transfer learning to handle limited input data. The advantages of transfer learning are its low computational cost and its ability to adapt pre-trained networks to similar feature prediction tasks.
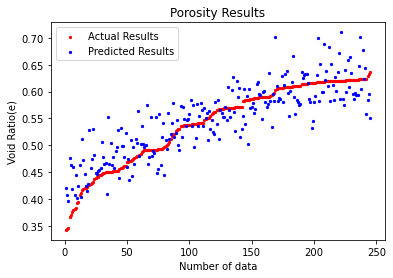
Additionally, special attention needs to be paid attention to the margin of error in our forecasts. In conventional deep learning research, the error rate obtained in this experiment ranges from minimum 0.0178% to a maximum of 23.13% (average = 5.69%), which can be considered to satisfy the project requirements. However, for void ratio regression predictions, this error percentage may not be small enough to validate the model ability, (i.e. Figure 1). Given that void ratio is a physical quantity that represents the ratio of pore volume to the total(solids) volume of a material, and that it always lies between 0 and 1, addressing the high variance of the prediction error range is a key goal for future work.
The Physical Information Neural Network PINN serves as an application method for scientific machines in the traditional numerical field, particularly in addressing a variety of challenges related to partial differential equations (PDE). These challenges encompass tasks such as equation solving, parameter inversion, model discovery, control, and optimization.
To enhance the prediction model for void ratio, it is crucial to incorporate physical information into the model. While many PINNs primarily focus on solving PDE-related problems, optimizing the prediction model for void ratio exploration into higher-order equation relationships associated with porosity or other high-dimensional fabric formulas. This approach is akin to the consideration of high-dimensional relationships in fields such as fluid dynamics or wave research. Exploring these higher-order equations and relationships in the context of materials mechanics represents a novel and promising direction worth further investigation.